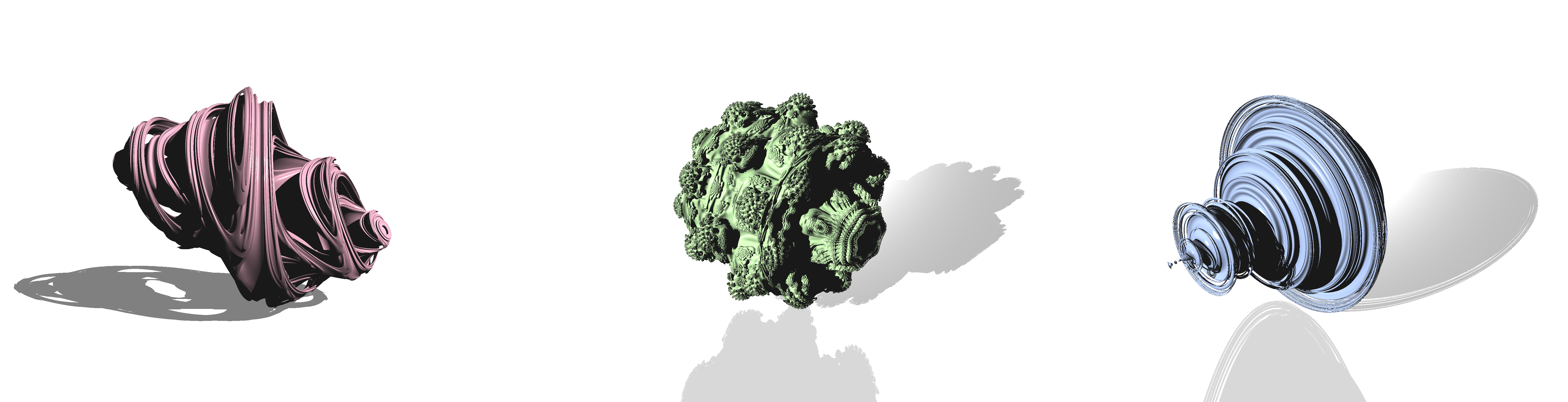
Rendering 3D Fractals by Sphere Tracing

こんにちは、研究チームの佐久間です。今日はアドベントカレンダー企画ということで、仕事の内容とは少し離れた、最近出会った面白い問題について書きたいと思います。

僕はコンピュータグラフィックスが専門ではないのですが、休日に GLSL (OpenGL Shading Language) を書いて書いて遊んだりしています。その中で Mandelbulb と呼ばれる奇妙なオブジェクトをレンダリングしている人たちがいることを知りました。

これが Mandelbulb です。単純なロジックから生まれる信じられないほど複雑なパターンを持つフラクタル図形であり、これをレンダリングしたいと強く惹かれましたが、この Mandelbulb のレンダリングについて原理と実装の両面から説明している文献は多くはありませんでした。今回はこのMandelbulb と関連するフラクタル図形をその背後にある原理に少し触れながら、実際にレンダリングしてみようと思います。

Mandelbrot Set / Julia Set

Mandelbulb の発端として、Mandelbrot 集合 / Julia 集合と呼ばれる複素平面上においてある性質を満たす点の集合があります。ある複素関数

$$
f_{c}(z)=z^{2}+c \tag{1}
$$

が与えられた時に、Mandelbrot 集合 $\mathcal{M}$, Julia 集合 $\mathcal{J}_{c}$ は以下で定義されます。

$$
\begin{align}
\mathcal{M}&=\{c: \lim_{n \to \infty} f^{n}_{c}(z) \not\to \infty\, , f'_{c}(z)=0\} \tag{2} \\
\mathcal{J_{c}}&=\{z: \lim_{n \to \infty} f^{n}_{c}(z) \not\to \infty\} \tag{3}
\end{align}
$$

これらはフラクタル図形としてはポピュラーであり、以下のような図形を目にしたことをある人は多いのではないかと思います。これは GLSL フラグメントシェーダにおいて Mandelbrot 集合なら各ピクセルを $c$, Julia 集合なら各ピクセルを $z$ として、$c, z$ がそれぞれ $c \in \mathcal{M}, z \in \mathcal{J}_{c}$ を満たすかどうかによって色付けすることで、いくらズームしても同じパターンが細部にまた現れる様子が確認できます。

2D Mandelbrot Set

See the Pen
2D Mandelbrot Set by Hiroki Sakuma (@skmhrk1209)
on CodePen.dark

2D Julia Set

See the Pen
2D Julia Set by Hiroki Sakuma (@skmhrk1209)
on CodePen.dark

冒頭の Mandelbulb は複素平面上でのMandelbrot 集合を3次元へ一般化する試みのようです。三元数というものは存在しないので、Mandelbrot 集合 / Julia 集合を四元数（クォータニオン）に拡張して、適当な超平面でスライスしてあげることで3次元の Mandelbrot 集合、Julia 集合を得ることができるようです。

ただ2次元の場合と異なり、3次元上の全ての点について Eq. (2), (3) が満たされるかどうかを調べることは現実的ではありません。ここで3次元のレンダリングは基本的に表面法線を計算することに帰着されることから、Mandelbrot 集合、Julia 集合の表面とピクセルから飛ばしたレイとの交点を求める問題を解きます。つまりレイトレーシングです。

Sphere Tracing

Mandelbrot 集合 / Julia 集合は Sphere Tracing / Ray Marching と呼ばれるレイトレーシングの亜種を用いてレンダリングすることができます。これは Signed Distance Function (SDF) と呼ばれる任意の3次元点を受け取り、そこから物体への最短距離を返す関数を用いてレンダリングするものです。

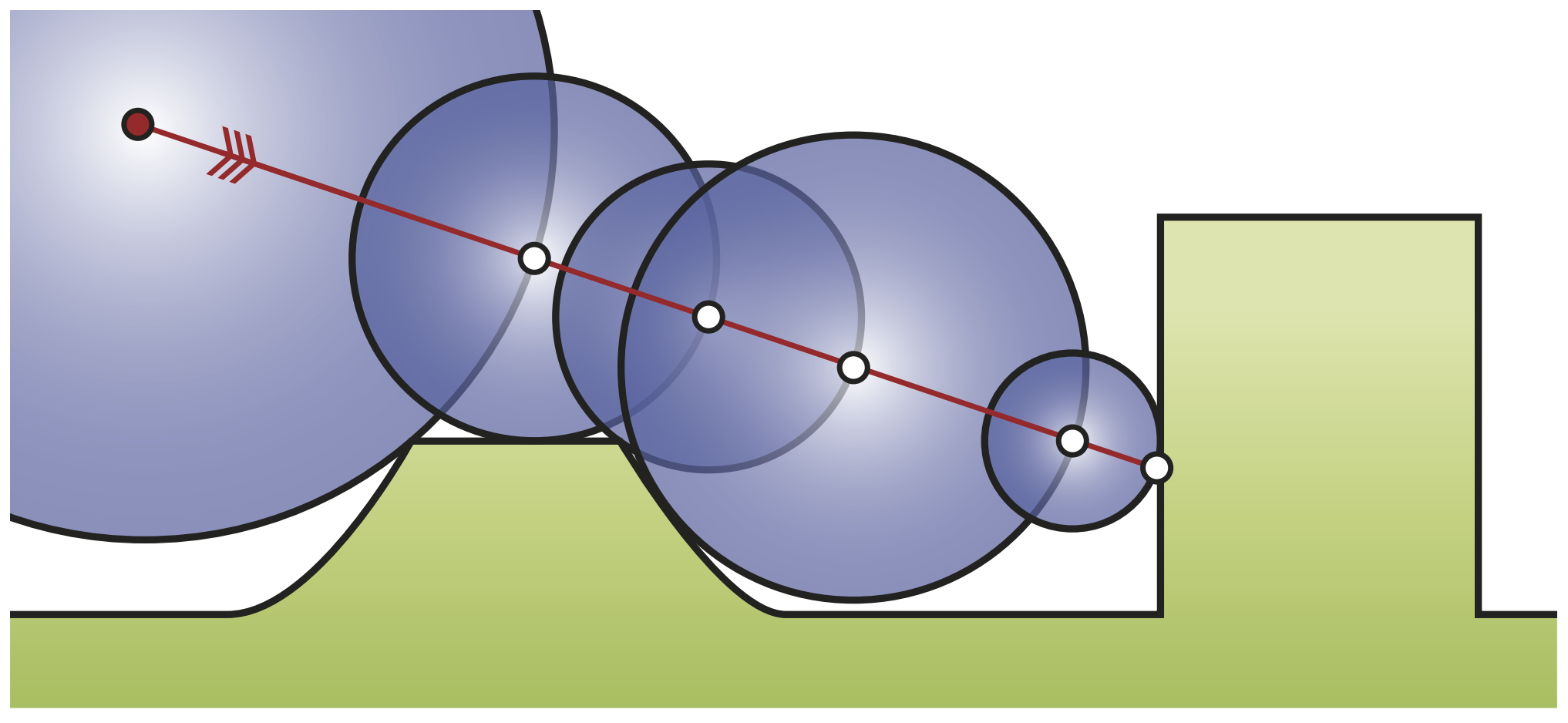
物体までの最短距離が分かれば、それを半径とする球を作ると、その球内には物体が存在しないことが保証されるので、何も気にせず、レイを進めることができます。SDF が 0 に収束したら、衝突したとみなしてその点を交点とします。

A basic implementation of sphere tracing [Keinert et al., 2014]^[1]

上記のコードを見るとわかるように Sphere Tracing は基本的にはイテレーション内で SDF を計算してその分だけレイを進める単純なアルゴリズムです。交点が求まると、法線を求めるのは簡単です。$\{p|\text{SDF}(p)=0\}$ は物体表面の陰関数表現となっており、陰関数の勾配 $\nabla{\text{SDF}}$ は法線であることから、有限差分などを用いて表面法線を求めることができます。

つまり Mandelbrot 集合 / Julia 集合の SDF が分かれば Sphere Tracing するだけでレンダリングできるのですが、残念ながらそのような都合の良いものは存在しません。ただここでのポイントは Sphere Tracing には必ずしも正確な SDF が必要というわけではないということです。要は物体に気づかずに通り過ぎなければ良いので、物体までの距離の下限さえ分かれば、パフォーマンスはともかく、Sphere Tracing することはできそうです。

Distance Estimator

The Orsay Notes [Douady and Hubbard, 1984]^[2] では、点 $z$ におけるJulia 集合 $\mathcal{J_{c}}$ に対するポテンシャル $G(z)$ を以下のように定義しています。
$$
G(z)=\lim_{n \to \infty}\cfrac{1}{2^{n}}\log|f_{c}^{n}(z)| \tag{4}
$$
$\mathcal{J_{c}}$ の定義から、$\mathcal{J_{c}}$ に含まれる点 $z$ で $G(z)=0$ となります。このポテンシャル $G(z)$ を用いると、$\mathcal{J_{c}}$ の外側のある点 $z$ から $\mathcal{J_{c}}$ の境界までの距離 $d(z)$ の bound は以下のように導かれます。
$$
\cfrac{\sinh{G(z)}}{2e^{G(z)}|G'(z)|}<d(z)<\cfrac{2\sinh{G(z)}}{|G'(z)|} \tag{5}
$$
The Science of Fractal Images [Barnsley et al., 1988]^[3] の Appendix D にここの導出が詳しく書いてあるので、数学が好きな人は見てみても良いかもしれません。実用上は $z$ が $\mathcal{J_{c}}$ に十分近いとして，
$$
d(z)>\cfrac{|{f_{c}}^{n}(z)|}{2|{f_{c}^{n}}'(z)|}\log|f_{c}^{n}(z)| \tag{6}
$$
とすることが多いようです。これで、Mandelbrot 集合 / Julia 集合の境界までの距離の下限が分かったので，Sphere Tracing により Mandelbrot 集合 / Julia 集合との交点を求めることができます。

ここで，${f_{c}^{n}}'(z)$ はどうやって求めれば良いのでしょう。これは入力、出力、ともにクォータニオンなので、ヤコビ行列と思われます。微分の仕方として、有限差分か自動微分が考えられますが、今回は双対数 (Dual Number) を用いたフォワード型の自動微分を実装しました。

Automatic Differentiation using Dual Numbers

双対数とは $\epsilon^{2}=0$ を満たす特殊な元 $\epsilon$ を導入した数のことです。実数 $a, b$ と $\epsilon$ を用いて $a+b\epsilon$ と表します。双対数には、その虚部が常に微分係数になるという性質があります。実際に $f(a+b\epsilon)$ をテイラー展開してみると

$$
\begin{align}
f(a+b\epsilon)&=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(b\epsilon)^{n}\\
&=f(a)+f'(a)b\epsilon+\sum_{n=2}^{\infty}\frac{f^{(n)}(a)}{n!}(b\epsilon)^{n}\\
&=f(a)+f'(a)b\epsilon
\end{align}
$$

つまり双対数の虚部 $b$ を，微分したい変数に関しては $1$，それ以外の変数に関しては $0$ にして関数に通すだけで、通常の関数の値に加えて、微分係数が計算できるという仕組みです。

ある実数を受けとる関数 $f$ を双対数バージョンにするのは簡単です。双対数を表すタプル $(g(x), g'(x))$ を受け取り、$(f(g(x)), f'(g(x))g'(x))$ を返せば良いです。双対数を一度実装すれば比較的エレガントに微分係数を求めることができそうです。

... おかしいですね、これはただの微分の連鎖率であり、双対数の概念は出てきません。双対数で自動的に微分係数が計算できるのは確かですが、テイラー展開して $\epsilon^{2}$ をあぶり出す操作をプログラムは知らないので、結局手で導関数を書き下すしかないのですね（何だそりゃ）。

これで全ての道具が準備できたので SDF の実装をすることができます。

Surface Normal

最後は法線の計算です。ポテンシャル $G(z)$ または推定距離 $d(z)$ の微分が計算できれば良さそうです。
$$
G(z)=\lim_{n \to \infty}\cfrac{1}{2^{n}}\log|f_{c}^{n}(z)| \tag{4}
$$ より，
$$
\nabla G(z)=\cfrac{1}{2^{n}|f_{c}^{n}(z)|}\nabla\sqrt{f_{c}^{n}(z)^{T}f_{c}^{n}(z)}=\cfrac{{f_{c}^{n}}'(z)^{T}f_{c}^{n}(z)}{2^{n}|f_{c}^{n}(z)|^{2}} \tag{7}
$$
となり、晴れて法線を求めることができそうです。あとは求めた法線を用いて、シェーディングをするだけです。今回はシンプルに Phong 反射モデルでシェーディングしてみました。

また、今回はリアルタイムデモのために OpenGL から WebGL に移行して、CodePen というサービスで HTML を埋め込んでみました。コードを編集してその効果を見たり、マウスで拡大したり、視点を変えたりできると思います。

3D Julia Set

See the Pen
3D Julia Set by Hiroki Sakuma (@skmhrk1209)
on CodePen.dark

3D Mandelbrot Set

See the Pen
3D Mandelbrot Set by Hiroki Sakuma (@skmhrk1209)
on CodePen.dark

Mandelbulb

実は冒頭の Mandelbulb は今回のクォータニオンで4次元に拡張した Mandelbrot 集合が見た目上あまり面白くないということで、幾何的な視点で再解釈したもののようです。確かに Julia 集合は興味深いビジュアルをしていますが、Mandelbrot 集合は対称性のせいか面白みに欠けますね。

そこで最後に Mandelbrot 集合を Mandelbulb に拡張してみます。Mandelbrot 集合におけるプロセスを再度眺めてみると、

$$
f_{c}(z)=z^{2}+c \tag{1}
$$

ここで $z$ は複素数であることから、$z^{2}$ は複素平面上で、原点からの長さを2乗し、角度を2倍にすることに対応します。ここで3元数なるものが存在しなくても、$z$ が3次元であるときに $z^{2}$ を3次元上で、原点からの長さを2乗し、角度を2倍にすることと解釈したらどうなるでしょう。この試みは成功し、Mandelbulb と呼ばれ人気のあるフラクタル図形の一つになりました。

実際には以下のように $f_{c}(z)=z^{n}+c$ に拡張することでさらに興味深いビジュアルになります。

$$
\begin{align}
(x, y, z) ^{n} &:= r^{n}(\sin(n\theta) * \cos(n\phi), \sin(n\theta) * \sin(n\phi), \cos(n\theta)) \tag{8} \\
\text{where} \ r &= \sqrt{x^{2} + y^{2} + z^{2}}, \ \theta = \arccos(z / r), \ \phi = \arctan(y / x) \\
\end{align}
$$

$n=8$ として実際にレンダリングしてみた結果が以下です。テクニカルなシェーディングは行っていないので、少し地味かもしれませんが、ポテンシャルを用いた距離推定で Julia 集合 / Mandelbrot 集合 / Mandelbulb をレンダリングすることができました。

Mandelbulb

See the Pen
Mandelbulb by Hiroki Sakuma (@skmhrk1209)
on CodePen.dark

以下のように単色での着色と簡単な影付け（物体交点からライトまで再びレイを飛ばして、交差判定をするだけ）をしてあげるだけでも結構いい感じですが、Orbit Traps^[4] と呼ばれる手法でフラクタルを着色することでより興味深いビジュアルになるようです。また今度挑戦してみようとおもいます。

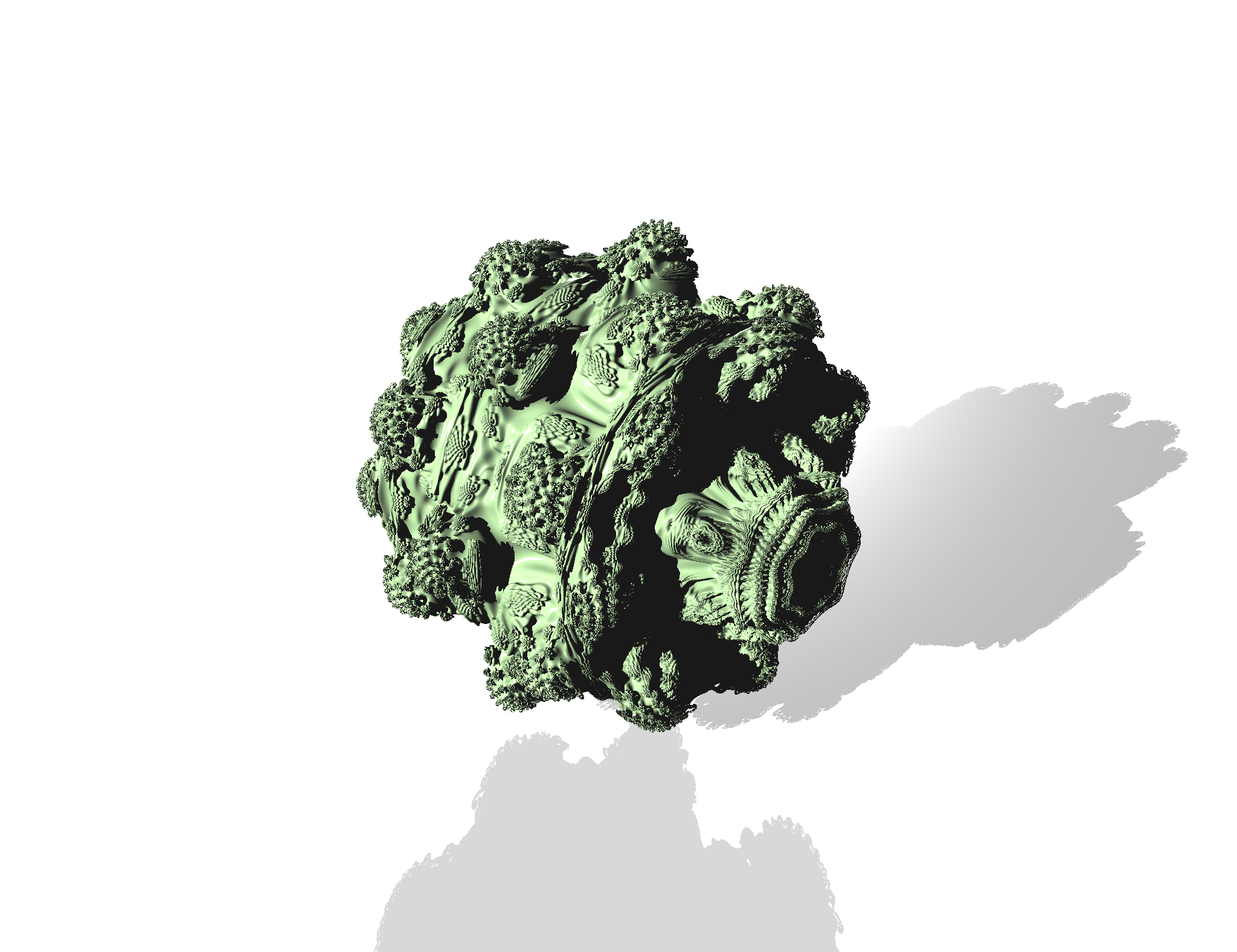
最後まで読んでくださり、ありがとうございました。

References

Keinert, Benjamin et al. “Enhanced Sphere Tracing.” STAG (2014).
Douady, Adrien, and John H. Hubbard. "Exploring the mandelbrot set. the orsay notes." Publ. Math. Orsay (1984).
Barnsley, Michael F., et al. The science of fractal images. Vol. 1. New York: Springer, 1988.
Quilez, Inigo. “ Geometric Orbit Traps .” Inigo Quilez, https://iquilezles.org/www/articles/ftrapsgeometric/ftrapsgeometric.htm.