Fit 4 arbitrary points as vertices of a rectangle

Hi, I am Zhang Qirui(張起瑞), a researcher working in SenseTime Japan.

I am a Chinese who have been living in Japan for ten years now, and still not feeling confident about writing technical contents in Japanese, ^1 With this blog writing chance I am going to share some interesting results from recent self-entertaining experiments.

This is about
Fit the RECTANGLE
Notebook link

This is about

making a rectangle out of 4 points.

Similar problems can be found in applications like softwares like Microsoft office lens, which retrieve an upright rectangle shape from a photo. It can recover the homography either by detecting the contour of 4 lines or 4 vertices.

Both ways, using the contours/points to recover the rectangle are equivelant to each other as dual problems. Because lines and points are duals under projective geometry. If the corner points and the contours are in good configuration, like forming a healthy convex hull, then this prolem is easy as we just need to estimate the homography to fit the shape into your desingated image pane or your cell phone screen.

Let's just think about some more difficult cases. What happens if the 4 points given is polluted in both of the following ways:

Affected by extreme measurement noise, the outline polygon formed by 4 points as vertices can be concave. In worst case this outline polygon can degenerate to a line.

In addition, the 4 points are not given in a clock/counterclock wise rotating maner, but in random order. Considering the all wrong correspondence, the configuration of 4 points sequence can be twisted([0,1,2,3]->[0,2,1,3]) or mirrored([0,1,2,3]->[0,3,2,1]) from the original topology.

Let's first take a look at some random generated ugly supposed to be rectangles.

w = 5
h = 3
gt_pts = np.array([
[-w/2,-h/2],
[w/2,-h/2],
[w/2,h/2],
[-w/2,h/2]
])
noise = np.random.rand(4,2)
m_pts = gt_pts + 1*min(h,w)*(noise-0.5)
theta = np.random.rand() * np.pi*2

rot = np.array([
    [np.cos(theta),np.sin(theta)],
    [-np.sin(theta),np.cos(theta)]
])

gt_pts = gt_pts @ rot.T
m_pts =  m_pts @ rot.T

order = [1,2,3]
random.shuffle(order)
m_pts[[1,2,3]] = m_pts[order]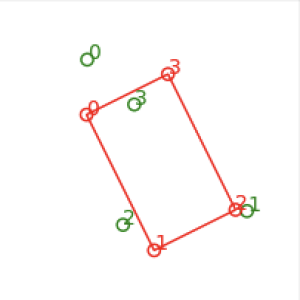

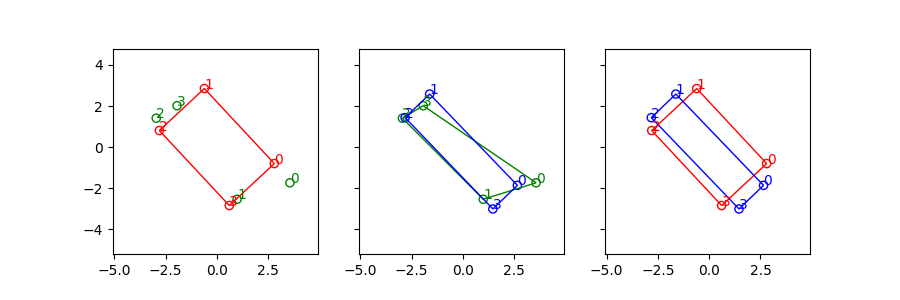
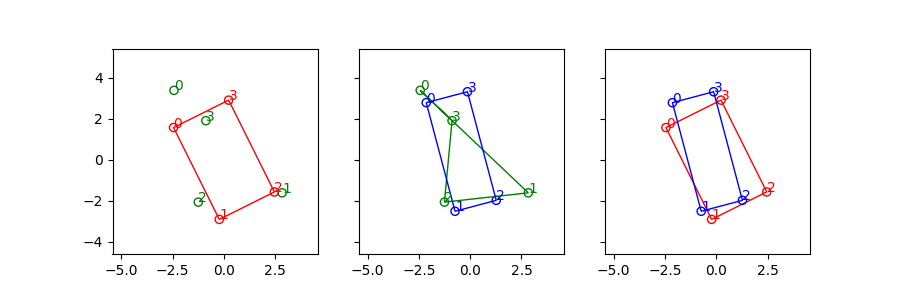
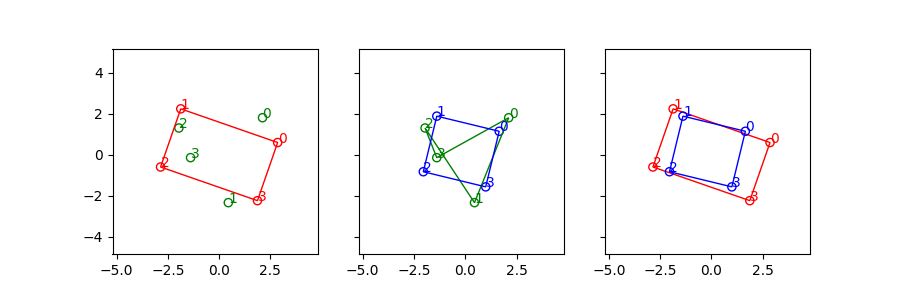
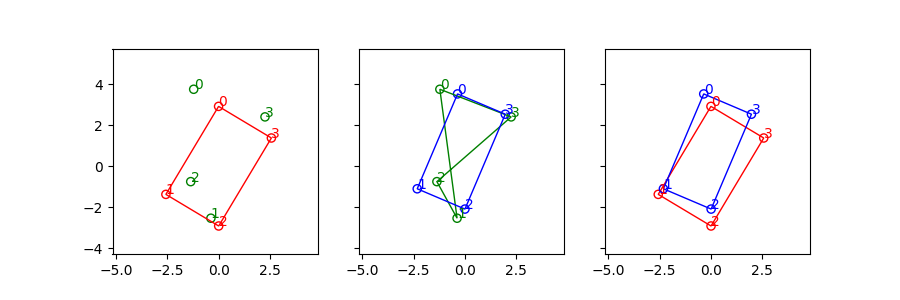
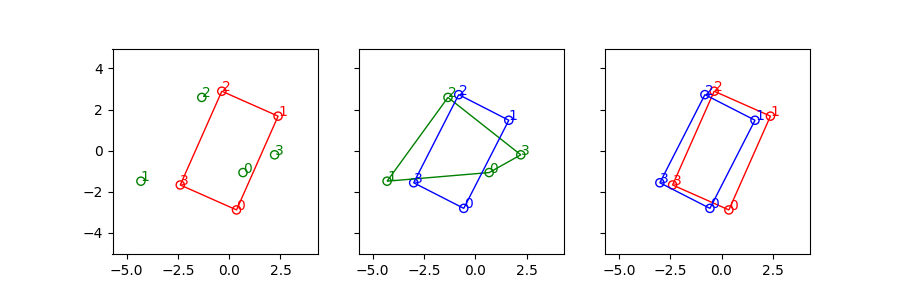
We can see the conifiguration of the green points(polluted vertices) are quite different from the red points(ground truth).
Then how to recover from such bad configurations?

Fit the RECTANGLE

Considering the orders of the points.
We are actually fitting a "directonal" rectangle into 4 ordered points.
For convinence, let's embed a counter-clockwise order into the 4 vertices of a unit square.

# matrix form: m_pts = Affine @ unit_square
# vector form: (x1,y1,x2,y2,x3,y3,x4,y4).T = square_prime @ [A[0], A[1], A[2], A[3]]
square_prime = np.array(
    [
        [-1,-1, 0, 0],
        [ 0, 0,-1,-1],
        [ 1,-1, 0, 0],
        [ 0, 0, 1,-1],
        [ 1, 1, 0, 0],
        [ 0, 0, 1, 1],
        [-1, 1, 0, 0],
        [ 0, 0,-1, 1]
    ]
)

Recover the correspondence

Without losing any generality, we can assign the 0 labeled point as the correctly corresponded sequence anchor.

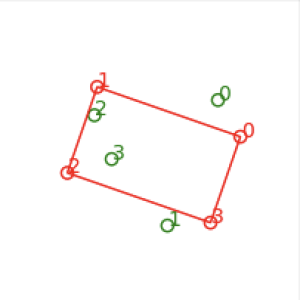
Then we try to recover the correct points correspondence from the original measurements. Since we already anchored one point, the correspondence possibility dropped from 4! permutations to 3! permutations. We simply compare the tendency of counter-clockwise rotation for each remaining point as if it is labeled 1.

The most potentially counter-clockwise rotating point is selected as 1 , and followed with the other 2 labels decided with same metric. If the rotation metric is close enough, it means the configuration is degenerated as a line and we will give up the rectangle fitting.

Results of correct correspondence by simply comparing the tendency of counter-clockwise rotation.

mean = m_pts.mean(0)
m_pts = m_pts - mean
rots = []
for i in range(1,4):
    line1 = m_pts[i] - m_pts[0]
    rot = 0
    for j in range(0,4):
        if i != j:
            line2 = m_pts[j] - m_pts[i]
            rot += np.cross(line2,line1)/(np.sqrt((line1**2).sum() * (line2**2).sum())+1e-5)
    rots.append(rot)
sorted_idx = np.argsort(rots)
if rots[sorted_idx[-1]] - rots[sorted_idx[0]] < 0.05:
    print("line? not even a triangle anyway")
m_pts[[1,2,3]] = m_pts[sorted_idx+1]

Recover the scale and the orientation

After this we can fit the unit square into these measurements using the corrected points correspondence.

By affine projecting the unit square into these 4 points, we can estimate the 2X2 affine transformation. Then we do the singular valude decompostion of the 2X2 affine matrix. The 2 singular value is the width and the heigh. And the orientation information in maintained in the 2 orthogonal matrices u/v. To notice that the determinant of u/v could be minus. Then we need switch the them in order to avoid flip.

    Affine_v = np.linalg.inv(square_prime.T @ square_prime ) @ square_prime.T @ m_pts.flat
    Affine = np.array([
        [Affine_v[0],Affine_v[1]],
        [Affine_v[2],Affine_v[3]]
    ])

    u,s,v = np.linalg.svd(Affine)
    print(u,s,v)

    scaling = np.array(s[0],s[1])

    if np.linalg.det(v) < 0:
        v[[0,1]] = v[[1,0]]
    if np.linalg.det(u) < 0:
        u[:,[0,1]] = u[:,[1,0]]

    rectangle = np.array([
        [-s[0],-s[1]],
        [s[0],-s[1]],
        [s[0],s[1]],
        [-s[0],s[1]]
    ])

    rectangle = (u @ v @ rectangle.T).T + mean

visualize the final result

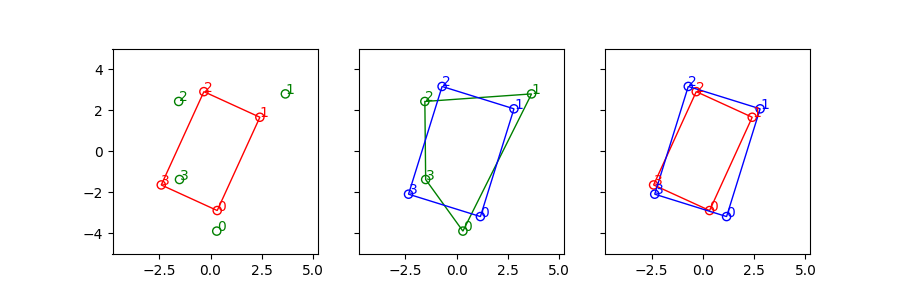
The green points are damaged observation of the red rectangle(Ground Truth). The blue rectangle is recovered rectangle from the green points. The process includes: